Según la suma de sus medidas, los ángulos se clasifican en ángulos complementarios y ángulos suplementarios. Vamos a estudiar ambos en esta clase, es muy fácil y te lo mostraré con algunos ejemplos.
Contenido
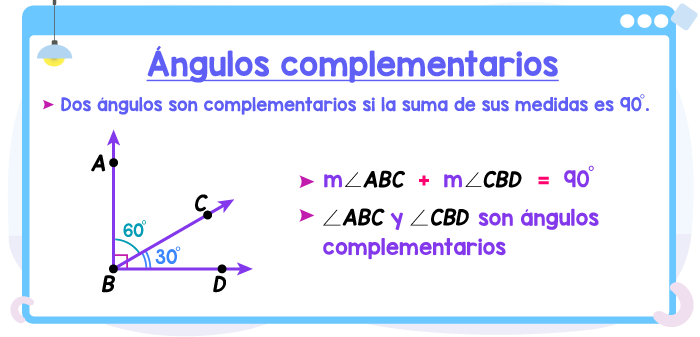
Ángulos complementarios
Dos ángulos son complementarios si la suma de sus medidas es 90°.
En la figura de abajo, ∠ABC y ∠CBD son ángulos complementarios pues la suma de sus medidas es 90°. También podemos decir que cada ángulo es el complemento del otro.
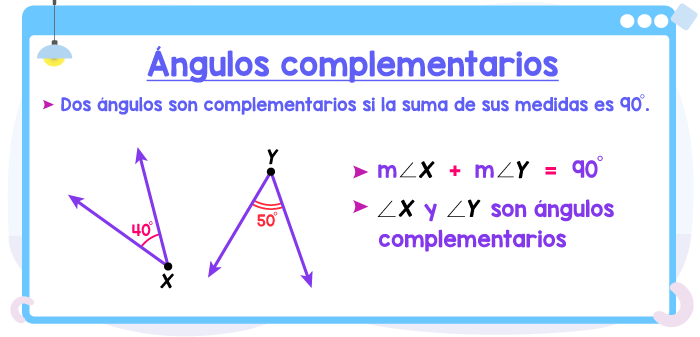
En este otro ejemplo, ∠X y ∠Y también son ángulos complementarios, debido a que si sumamos nos medidas, obtenemos 90°. Ten en cuenta que los ángulos complementarios no necesitan ser ángulos adyacentes. Recuerda que los ángulos adyacentes son aquellos que tienen un vértice común y un lado común entre ellos.
Ángulos suplementarios
Dos ángulos son sumplementarios si la suma de sus medidas es 180°.
En la siguiente figura, ∠MON y ∠NOP son ángulos suplementarios, debido a que la suma de sus medidas es 180°. También podemos decir que cada ángulo es el suplemento del otro.

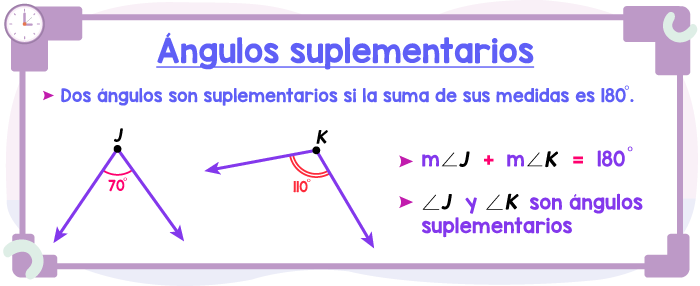
Y en este otro ejemplo, ∠J y ∠K son ángulos suplementarios, pues si sumamos sus medidas obtenemos como resultado 180°. Los ángulos suplementarios no necesitan ser ángulos adyacentes.
Videos
En el siguiente video veremos más ejemplos de ángulos complementarios y suplementarios.
A continuación, viene un ejercicio de ángulos suplementarios:
Referencias
Para esta clase, hemos usado estas referencias.
- Alexander, D. y Koeberlein, G. (2013). Geometría (5.ª e d.; pp. 34-35). Cengage Learning.
- Tussy, K., Gustafson, D. y Koenig, D. (2013). Matemáticas básicas (4.ª ed.; pp. 718-720). Cengage Learning.