Para hallar la fracción de número o cantidad, se divide dicho número entre el denominador y el resultado se multiplica por el numerador. Veamos algunos ejemplos para que esto se termine de entender.
Contenido:
1) Hallar 1⁄4 de 20:
Primero dividimos 20 entre el denominador (4), al final, el resultado lo multiplicamos por el numerador (1).

La respuesta es 5.
2) Hallar 2⁄3 de 21:
Recuerda que primero dividimos 21 entre el denominador (3), después, el resultado lo multiplicamos por el numerador (2).

El resultado sería 14. También puedes resolver el ejercicio de forma gráfica (con ayuda de una barra) y obtendrás el mismo resultado.
3) Hallar 3⁄5 de 60:
Empezamos dividiendo 60 entre el denominador (5), después, el resultado lo multiplicamos por el numerador (3).
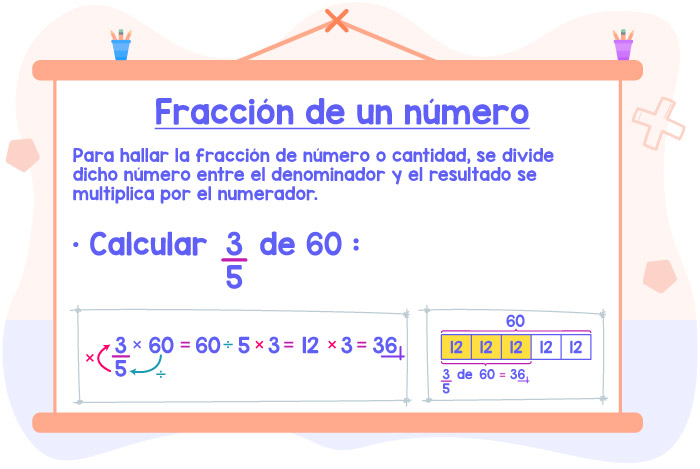
El resultado es 36.
Por último, tengo que aclarar que, si decides cambiar el orden de las operaciones, es decir, primero multiplicas por el numerador y al final divides entre el denominador, el resultado sería el mismo, así que no te asustes.
Video
En el siguiente video, veremos algunos ejemplos más en los que calcularemos la fracción de un número.
Referencias
Para esta clase, hemos usado las siguientes referencias:
- Neagoy, M. (2017). Unpacking fractions: classroom-tested strategies to build students’ mathematical understanding. ASCD/National Council of Teachers of Mathematics (NCTM).
- Baldor, A. (2017). Aritmética (3.ª ed., p. 270). Grupo Editorial Patria.
- Santillana Perú (2019). Resuelve: matemática 5° de primaria (p. 45).
- Santillana Perú (2019). Resuelve: matemática 6° de primaria (p. 40).
Nota para profesores
En este clase hemos trabajado con el significado de la fracción como operador. De acuerdo con Neagoy (2017), cuando se multiplica un número o una cantidad por la fracción a⁄b, se realizan dos pasos, primero se multiplica el número o cantidad por el numerador a y luego se divide por el denominador b, aunque el orden se puede invertir.