Distribución binomial, ejercicios resueltos

La distribución de probabilidad binomial es una distribución discreta que tiene muchísimas aplicaciones. Se asocia con un experimento de múltiples pasos que se llama experimento binomial. La palabra binomial viene de otra palabra que significa “dos nombres” y esto nos hará recordar que en cada ensayo que veremos en este tema siempre habrá dos resultados: éxito y fracaso. Si es que respondes una pregunta de alternativas al azar, la respuesta es correcta o incorrecta. Si es que realizas un control de calidad a un producto, este será defectuoso o no defectuoso. Si es que lanzas una moneda, sale cara o sale cruz.

Veamos a detalle la distribución binomial, su fórmula y por supuesto, muchos ejercicios.

Contenido

1) Experimento binomial.
2) Las hamburguesas de Jorge.
3) Función de probabilidad binomial (fórmula).
4) Media, varianza y desviación estándar de la distribución binomial.
5) Ejemplos
6) Guía de ejercicios.
7) Video de introducción.
8) Referencias.

Para estudiar esta distribución binomial, empezaremos conociendo los experimentos binomiales, como, por ejemplo, el lanzamiento de una moneda.

1) Experimento binomial

Un experimento binomial es un experimento que cumple las siguientes condiciones:

i) El experimento consta de una secuencia de n ensayos idénticos.
ii) En cada ensayo hay dos resultados posibles. A uno de ellos se le llama éxito y al otro, fracaso.
iii) La probabilidad de éxito es constante de un ensayo a otro, nunca cambia y se denota por p. Por ello, la probabilidad de fracaso será 1 – p. Esto se debe a que la probabilidad de éxito más la probabilidad de fracaso suman 1.
iv) Los ensayos son independientes, de modo que el resultado de cualquiera de ellos no influye en el resultado de cualquier otro ensayo.

Antes de resolver un ejercicio aplicando la fórmula de probabilidad binomial, tenemos que verificar siempre que se cumplen estas cuatro condiciones, pues esta fórmula solo funciona para experimentos binomiales.

Esta ya se está poniendo muy aburrido, mejor veamos un ejemplo. 

2) Las hamburguesas de Jorge

Últimamente con las clases de matemática no me va muy bien, por eso, he puesto mi cafetería. Preparo unas cosas riquísimas, pasteles, pizza, agua helada, pero lo más vendido son las matehamburguesas, las únicas hamburguesas que se venden con papas y leche chocolatada.

La probabilidad de que a un cliente nuevo le guste la matehamburguesa es de 0,8. Si vienen 3 nuevos clientes a mí cafetería ¿cuál será la probabilidad de que solo a dos de ellos les guste la hamburguesa?

Si al cliente le gusta la hamburguesa tendrá carita feliz y si no le gusta, tendrá carita molesta. Por ejemplo, si a los dos primeros les gusta y al tercero no, colocaré esta gráfica:

Pero no es la única opción, en total son tres opciones. Que a los dos primeros les guste y al tercero no. Que al primero y al tercero les guste, y al segundo no. O que les guste al segundo y tercero y al primero no. Graficamos estas tres opciones:

Si la probabilidad de que a un cliente le guste la matehamburguesas es de 0,8, entonces, la probabilidad de que no le gusten será:

Ahora calcularemos la probabilidad de que ocurra cada evento. Por ejemplo, en la primera línea, calcularemos la probabilidad de que al primer y al segundo cliente les guste la hamburguesa y que al tercero no. Aplicaremos la regla de la multiplicación de probabilidades para eventos independientes.

Coloco ahora todas las opciones.

Esas mismas probabilidades, las colocaré en forma de potencias:

Me quedaré solo con las potencias, eliminando el resto.

A continuación, calculamos la probabilidad total de que solo a 2 de los 3 clientes les guste mi hamburguesa empleando la regla de la suma de probabilidades para eventos mutuamente excluyentes.

Si esta multiplicación la metemos a la calculadora, nos quedaría 0,384.

¿Es un poco largo este cálculo? Pues sí, está larguísimo. Imagínate que ahora llegan 10 clientes nuevos a mi cafetería y queremos calcular la probabilidad de que a 4 de ellos les guste la matehamburguesa. Me tardaría horas, por eso es mejor usar la fórmula de la función de probabilidad binomial.  Esta fórmula permite encontrar la probabilidad para cada posible valor de x (número de éxitos). Veamos los detalles:

3) Función de probabilidad binomial (fórmula)

Para un experimento binomial, sea p la probabilidad de “éxito” y 1-p la probabilidad de un “fracaso” en un solo ensayo; entonces la probabilidad de obtener x éxitos en n ensayos, está dada por la función de probabilidad f(x):

Siendo el coeficiente binomial o número combinatorio:

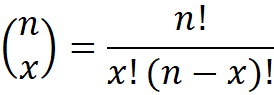
Por eso, en algunos libros encontrarás la función de probabilidad binomial f(x) con el coeficiente binomial ya incorporado y presentada de la siguiente manera:

¿Cuál de las formas es la mejor? Eso ya depende de lo que diga tu corazón, pero recuerda que el resultado es el mismo.

La función de probabilidad binomial se aplica a cualquier experimento binomial. Si una situación demuestra las propiedades de un experimento binomial y se conocen los valores de n y p, se puede usar la ecuación de arriba para calcular la probabilidad de x éxitos en n ensayos. Recuerda, antes de usar la fórmula de probabilidad binomial, siempre verifica que te encuentres ante un experimento binomial.

4) Media, varianza y desviación estándar de la distribución binomial

La media, la varianza y la desviación estándar se pueden encontrar con estas fórmulas:

Media:

Varianza:

Desviación estándar:

5) Ejemplos

La probabilidad de que a un cliente nuevo le guste la matehamburguesa de Jorge es de 0,8. Si llegan 5 clientes nuevos a la cafetería, ¿cuál es la probabilidad de que solo a 3 de ellos les guste la matehamburguesa?

Solución:

Antes de aplicar la fórmula, verificamos que se trate de un experimento binomial. Para ello, tiene que cumplir con las 4 condiciones que mencionamos arriba. Efectivamente, se trata de un experimento binomial.

En este caso, vamos a centrarnos en los clientes a los que les gusta esta hamburguesa, por ello diremos que:

X = número de clientes nuevos de 5 a los que les gusta la matehamburguesa

Entonces consideramos un éxito si al cliente le gusta esta hamburguesa.

Aplicaremos la fórmula binomial:

Ahora colocamos los valores de n, k y p. Recuerda que n es el número de ensayos, k el número de éxitos y p la probabilidad de éxito.

Reemplazamos estos valores en la fórmula:

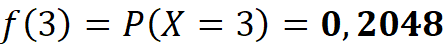
La respuesta sería 0,2048.

Recuerda que X, nuestra variable aleatoria, es el número de clientes nuevos de 5 a los que les gustan las hamburguesas de Jorge. Aunque el problema no lo pide, vamos a elaborar la tablita de distribución de probabilidad. Para calcular todas las probabilidades, usaré la misma fórmula de arriba.

Vamos a elaborar una gráfica para representar esta distribución de probabilidad, empleando un diagrama de barras.

Algunos usan los histogramas, también es válido.

Ejemplo 2

De todas las flores plantadas por una empresa de jardinería, el 90% sobrevive. Si se plantan 10 flores ¿cuál es la probabilidad de que 9 o más sobrevivan?

Solución:

Antes de aplicar la fórmula, verificamos que se trate de un experimento binomial. Para ello, tiene que cumplir con las 4 condiciones que mencionamos arriba. Efectivamente, se trata de un experimento binomial.

En este caso, vamos a centrarnos en las flores que sobreviven, por ello diremos que:

X = número de flores de 10 que sobreviven

Entonces consideramos un éxito si la flor sobrevive. A las que flores que se mueren, las consideramos como un fracaso.

Aplicaremos la fórmula binomial:

Nos piden calcular la probabilidad de 9 o más sobrevivan.

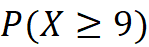
Este problema tiene trampa, porque dado que se plantaron 10 flores, la máxima cantidad de flores que pueden sobrevivir es 10, por lo tanto:

– ¿Y no pueden sobrevivir 11 flores?
– No se puede, porque solo se plantaron 10.
– ¿Y si las flores tienen hijitos bonitos?
– Alumno por favor, tome menos azúcar. Concéntrese y sigamos con la clase.

Ahora colocamos los valores de n, k y p. Recuerda que n es el número de ensayos, k el número de éxitos y p la probabilidad de éxito. En este caso:

Regresamos con la fórmula de arriba:

Vamos a calcular cada probabilidad por separado, empezando con P(X = 9):

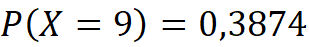
Continuamos con P(X = 10).

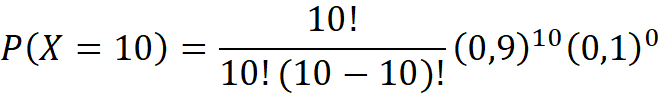
Regresamos con esta fórmula:

Y reemplazamos lo calculado:

Ejemplo 3

Considere un experimento binomial con dos ensayos y p=0,4.
a) Calcular la probabilidad de no obtener ningún éxito.
b) Calcular la probabilidad de obtener al menos 1 éxito.

Solución:

Iniciamos definiendo la variable aleatoria de interés en nuestro experimento binomial:

X = número de éxitos en n ensayos.

x = 0; 1; 2.

El enunciado nos dice que: n = 2 y que p = 0,4; con ello podemos definir la función de probabilidad de X.

a) Calcular la probabilidad de no obtener ningún éxito: P(X = 0).

b) Calcular la probabilidad de obtener al menos 1 éxito.

Aquí nos piden calcular:

Pero:

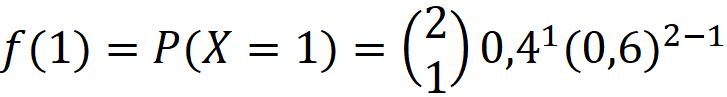
Además:

Reemplazamos:

Esa sería la respuesta: 0,64.

Una forma alternativa de desarrollar el apartado b, sería usando la siguiente

“La suma de las probabilidades para todos los resultados del experimento debe ser igual a 1”.

Pero recuerda que P(X=0) ya lo calculamos en el apartado a, y es igual a 0,36.

6) Guía de ejercicios

Desde el botón que viene a continuación, podrás descargar la guía de ejercicios de distribución binomial.

7) Video de introducción

A continuación, viene la primera clase de distribución binomial, en la cual realizamos la introducción y resolvemos un problema bien interesante.

En este enlace, encontrarás muchas otras clases y videos de distribución binomial. 

8) Referencias

Para elaborar este artículo y los videos de arriba, hemos empleado los siguientes libros:

• Anderson, D., Sweeney, D. y Williams, T., 2012. Estadística para negocios y economía. 11a ed. Ciudad de México: Cengage Learning, pp.207-221.
• Johnson, R. y Kuby, P., 2012. Estadística elemental. 11a ed. Ciudad de México: Cengage Learning, pp.243-262.
• Navidi, W. (2006). Estadística para ingenieros. 1a ed. México: McGraw-Hill, pp.195-206.